01a. PEN K12 (Canada 1969) Find all functions such that for all
:
,
,
.
01b. Let be a function satisfying the conditions:
(a) for all relatively prime
and
, and
(b) for all positive integers
.
Show that there is a constant such that
for all
.
Here is the official solution: PEN01S
An alternative solution is here: CMO 2003 (problem 4)
You can also disscuss the problems here!
References
[1] P. Erdos, On the distribution function of additive functions, Ann. of Math., 47(1946), 1-20
[2] E. Howe, A new proof of Erdos’s theorem on monotone multiplicative functions, Amer. Math. Monthly, 93(1986), 593-595
[3] L. Moser and J. Lambek, On monotone multiplicative functions, Proc. Amer. Math. Soc., 4(1953), 544-545
Acknowledgement. We would like to express our gratitude to Andrei Frimu who helped us preparing the solutions and Orlando Doehring who offered me the solution file of CMO 2003.
I guess the first solution for 01a is not valid. How do you prove that is the only solution? The induction steps prove that the function works, but they don’t prove that no other function works as well.
is the only solution? The induction steps prove that the function works, but they don’t prove that no other function works as well.
The solution is valid. The induction step does not simply prove that works, but that
works, but that 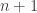 is the only possible value
is the only possible value  can take.
can take.